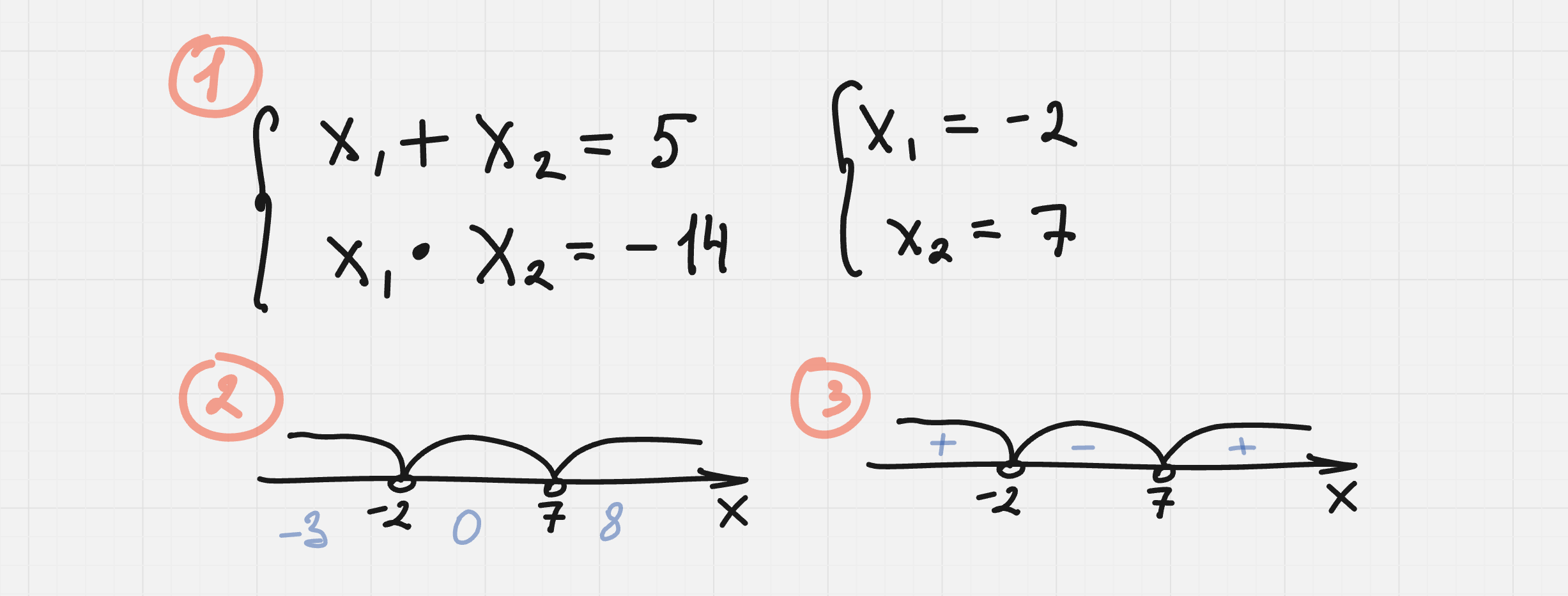Решение неравенств. Метод интервалов
Метод интервалов применяют для решения неравенств, но сначала разберёмся в азах.
Для записи неравенств используют знаки: > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Нестрогое неравенство допускает, что переменная может быть равна заданному числу. При записи ответа со строгим неравенством используют круглые скобки (2; 3)
Нестрогое неравенство — ответ может быть равен заданному числу. При записи ответа с нестрогим неравенством используют квадратные скобки [2; 3]
Как правильно поставить знак неравенства? Представим его в виде открытого рта. Рот мы открываем в сторону большего числа, так как хотим кусок торта побольше.
Для записи неравенств используют знаки: > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Нестрогое неравенство допускает, что переменная может быть равна заданному числу. При записи ответа со строгим неравенством используют круглые скобки (2; 3)
Нестрогое неравенство — ответ может быть равен заданному числу. При записи ответа с нестрогим неравенством используют квадратные скобки [2; 3]
Как правильно поставить знак неравенства? Представим его в виде открытого рта. Рот мы открываем в сторону большего числа, так как хотим кусок торта побольше.
3-и больше 2-х: 3 > 2
I. Решения неравенств через совокупность систем
Рассмотрим два случая, когда выражение меньше и больше нуля.
1. Меньше нуля:
1. Меньше нуля:
(x-3)(x-7)<0
Два выражения представлены в виде произведения.
А когда наше произведение меньше нуля?
Тогда, когда одно число меньше нуля, а другое больше, из чего записываем пары совокупностей:
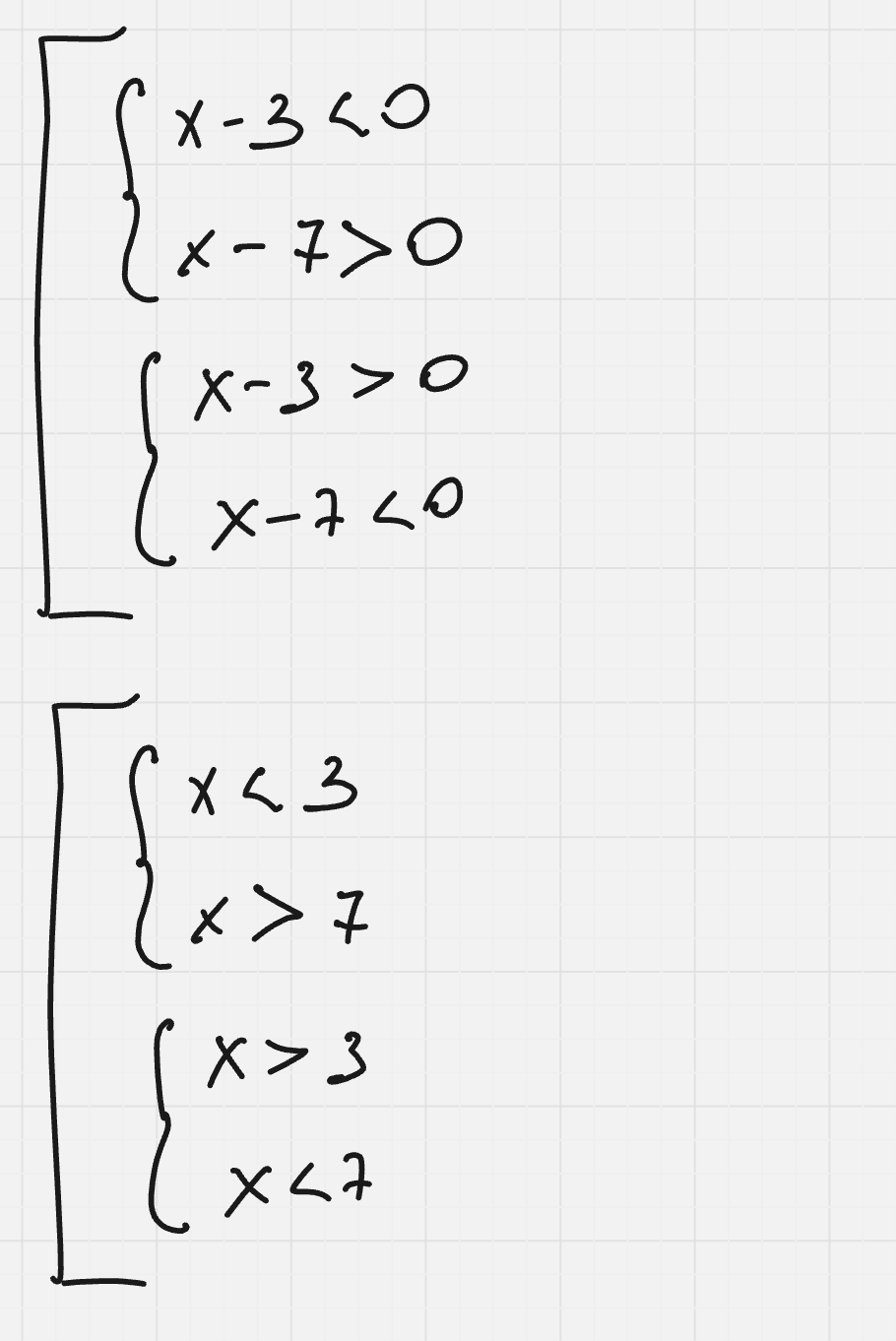
Проверяем, какая из систем удовлетворяет решению неравенства, подставляя числа из промежутков:
x < 3 (2-3)(2-7) = 15; 15 > 0 не подходит
x > 7 (8-3)(8-7) = 5; 5 > 0 не подходит
x > 3 (4-3)(4-7) = –9; –9 < 0 подходит
x < 7 (6-3)(6-7) = –21; –21 < 0 подходит
x > 7 (8-3)(8-7) = 5; 5 > 0 не подходит
x > 3 (4-3)(4-7) = –9; –9 < 0 подходит
x < 7 (6-3)(6-7) = –21; –21 < 0 подходит
Ответ: x ∈ (3; 7)
2. Больше нуля:
Два выражения представлены в виде произведения.
(x-10)(x-15) > 0
Два выражения представлены в виде произведения.
А когда наше произведение больше нуля?
Тогда, когда оба числа либо меньше нуля, либо больше нуля, из чего создаем пары совокупностей:
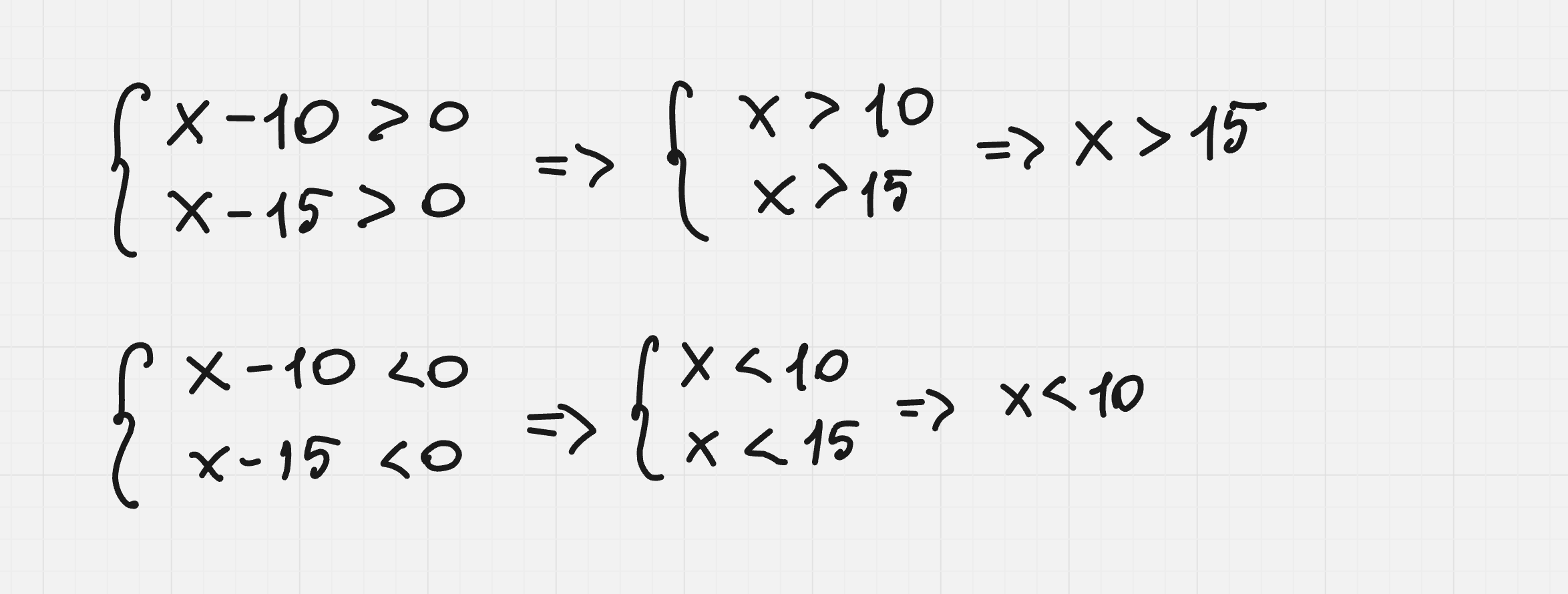
Ответ: x ∈ (– ∞; 10) ∪ (15; ∞)
II. Решения неравенств с помощью метода интервалов
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения:
1. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2. Найти нули функции(корни уравнения), для этого необходимо решить уравнение прировняв неравенство к нулю.
3. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное число из интервала вместо неизвестной. Если в результате получится положительное число, то и интервал будет положительным. Если же ответ окажется отрицательным, то и интервал будет отрицательным.
1. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2. Найти нули функции(корни уравнения), для этого необходимо решить уравнение прировняв неравенство к нулю.
3. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное число из интервала вместо неизвестной. Если в результате получится положительное число, то и интервал будет положительным. Если же ответ окажется отрицательным, то и интервал будет отрицательным.
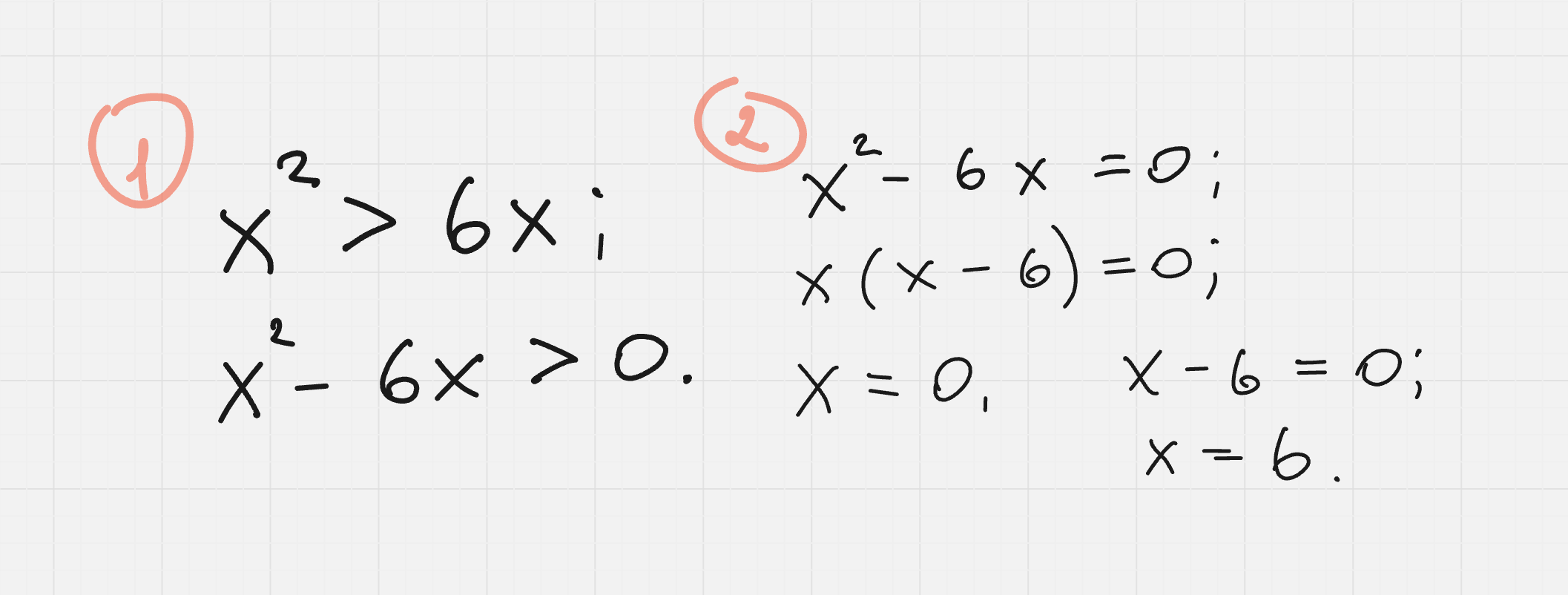
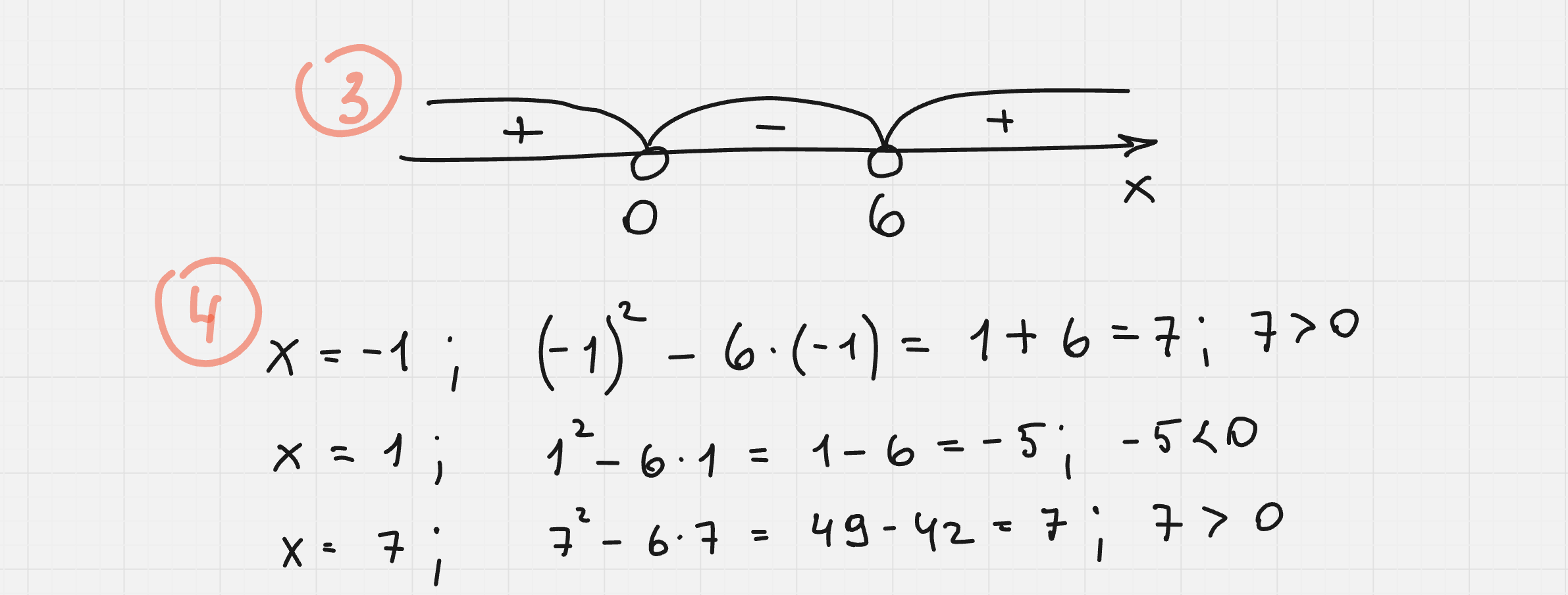
Выражение x² – 6x > 0 должно быть больше нуля.
Смотря на числовую прямую мы видим удовлетворяющие нас интервалы на промежутках
(– ∞; 0) ∪ (6; ∞)
Ответ: x ∈ (– ∞; 0) ∪ (6; ∞)
Пример:
x² – 5x – 14 > 0
1. Найдём корни
Решим уравнение x² - 5x - 14 = 0
x = –2, x = 7
2. Чертим числовую прямую и отмечаем на ней корни
3. Определяем знаки на интервалах
x = – 3, (-3)²–5(–3)–14=10, 10 > 0
x = 0, (0)²–5(0)–14=–14, –14 < 0
x = 8, (8)²–5(8)–14=10, 10 > 0
x = – 3, (-3)²–5(–3)–14=10, 10 > 0
x = 0, (0)²–5(0)–14=–14, –14 < 0
x = 8, (8)²–5(8)–14=10, 10 > 0
4. Итоги
Неравенство x² – 5x – 14 > 0 должно быть больше нуля.
Ответ: x ∈ (– ∞; –2) ∪ (7; ∞)